Különbség a határozott és a határozatlan integráció között A különbség
számként ismert. A számítás a matematika egyik fontos ágát jelenti, és a differenciálás kritikus szerepet játszik a számításban. A differenciálódás inverz folyamata integrációnak nevezhető, az inverz pedig integránsnak nevezhető, vagy egyszerűen csak a differenciálódás inverzét alkotja. Az általuk készített eredmények alapján az integrálok két osztályba sorolhatók., határozott és határozatlan integrál.
Definite Integral
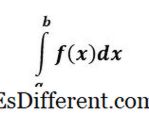
definíciója f (x) definíciója egy szám, és a f (x) görbe alatti területet jelenti x = a , hogy x = b .
Egy meghatározott integrálnak van az alsó és felső határ az integrálokon, és ez határozott, mert a probléma végén van egy számunk - ez határozott válasz.
-2 ->Határozatlan Integrál

Az f (x) meghatározatlan integrálja egy FUNKCIÓ, és azt a kérdést adja meg, hogy "Mi különbözteti meg a funkciót f (x) ? "
Határozatlan integrációval itt nincsenek felső és alsó határértékek az integrálra, és amit kapunk, a válasz még mindig x ben van, és állandó (amelyet általában C jelölik.
A határozatlan integrál általában általános megoldást ad a differenciálegyenletre.
A meghatározatlan integrál sokkal inkább az integráció általános formája, és a megfontolt funkció anti-származékaként értelmezhető.
Tegyük fel, hogy a függvény F differenciálódása egy másik függvényhez vezet f , és az integráció integrálja. Szimbolikusan ez a szöveg
F (x) = ∫ƒ (x) dx
vagy
F = ∫ƒ dx
esetén mindkettő F és függvények x és F különböztethetőek. A fenti formában Reimann integráltnak nevezzük, és az eredményül kapott függvény önkényes konstansot tartalmaz. Határozatlan integrál gyakran létrehoz egy funkciócsoportot; ezért az integrál meghatározatlan.
Az integrációk és az integrációs folyamat a differenciálegyenletek megoldásának középpontjában áll. Azonban a differenciálás lépéseitől eltérően az integráció lépései nem mindig követik a világos és standard rutinokat. Alkalmanként azt látjuk, hogy a megoldást nem lehet explicit módon kifejezni az elemi funkció szempontjából. Ebben az esetben az analitikus megoldást gyakran határozatlan integrál formájában adják meg.
A kalkulus alapvető elmélete
A határozott és a határozatlan integrál a Kalkulus Alapelmélete alapján kapcsolódik össze:
definite integral kiszámításához határozatlan integrál > (más néven anti-származék) és értékeli a x = a és x = b végpontokban. A határozott és határozatlan integrálok közötti különbség akkor lesz nyilvánvaló, ha egyszerre értékeljük az integrálokat ugyanarra a funkcióra.
Tekintsük a következő integrált értéket:
OK. Csináljuk mindkettőt, és nézzük meg a különbséget.

Az integrációhoz meg kell adnunk az egyiket az indexhez, amely a következő kifejezéshez vezet:
Ebben az időpontban
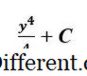
C csak számunkra állandó. További információ szükséges a probléma során a C pontos érték meghatározásához. Értékeljük ugyanazt az integrált definíciót i. e., a felső és az alsó határértékek között.
Grafikailag most a

f (x) = y 3 görbe alatt a y = 2 és y = 3 >. Az értékelés első lépése megegyezik a határozatlan integrálértékeléssel. Az egyetlen különbség az, hogy ezúttal nem adjuk hozzá az állandó C
értéket. Ebben az esetben a kifejezés a következőképpen néz ki: Ez a sor következik:
Lényegében 3, majd 2 helyettesítjük a kifejezést, és megkaptuk a különbséget közöttük.

Ez határozott érték, szemben az állandó

C
korábban. Vizsgáljuk meg az állandó tényezőt (a határozatlan integrálást illetően) még részletesebben.
y
3 3y 2 különbség ∫ 3y
2 dy = y 3 Mindazonáltal 3y
2 különbözõ kifejezések különbsége lehet, amelyek közül néhány y 3 -5 , > y 3 +7 stb. Ez azt jelenti, hogy a megfordítás nem egyedi, mivel az állandó a művelet során nem található meg. Tehát általában 3y 2
az y 3 + C különbség, ahol C bármely állandó. Egyébként C a "integrációs állandó" néven ismert. Ezt a következőképpen írjuk: ∫ 3y
2
. dx = y 3 + C Az integrálási technikák meghatározatlan integrálissá, például az asztalkereséshez vagy a Risch integrálásához új szüneteket adhatnak az integrációs folyamat során. Ezek az új diszkontinuitások azért jelennek meg, mert a származék-származékok komplex logaritmus bevezetését igényelhetik. A komplex logaritmusok folytonossági megszakítással rendelkeznek, amikor az argumentum átkerül a negatív valós tengelyre, és az integrációs algoritmusok néha nem találnak olyan ábrázolást, ahol ezek az ugrások megszakadnak.
Ha a meghatározatlan integrált értéket először egy meghatározatlan integrál számításával értékeljük, majd az integrációs határokat az eredménybe helyezzük, tisztában kell lennünk azzal, hogy a határozatlan integráció diszkontinuitást eredményezhet. Ha igen, akkor meg kell vizsgálnunk az integrációs intervallumban tapasztalt megszakításokat.




