Különbség a származékos és a differenciál
Származékos és differenciál
A differenciál-kalkulusban a függvény származtatása és differenciálódása szorosan összefügg egymással, de nagyon különböző jelentéseik vannak; amelyet a különböző funkciókhoz kapcsolódó két fontos matematikai objektum képvisel.
Mi a származék?
Egy függvény szekvenciája azt a mértéket méri, amellyel a függvényérték megváltozik, ahogy a bemenet változik. A többváltozós függvényekben a függvényérték változása a független változók értékeinek változásának irányától függ. Ezért ilyen esetekben egy adott irány kiválasztásra kerül, és a funkció ebben a meghatározott irányba differenciálódik. Ezt a származékot irányszármazéknak nevezik. A részleges származékok speciális irányszármazékok.
-1 ->Egy vektorértékű függvény f származékát definiálhatjuk


mindenhol differenciálható, és a származék egyenlő a





Ez az első származék. Általában a f funkció első származékát f (1) jelöli. Most ezt a jelölést használva lehetőség van magasabb rendű származékok definiálására. a másodrendű irányított származék, és a
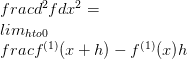

x
egy adott függvény f függvényére az 1 df összesített eltérése. Ez azt jelenti, hogy a x

x és a f tetszőleges pontban x változás a f. Megmutatható, hogy a Δ f = f (1) (x ) x + ε, a hiba. A Δ f / Δ x = f (1) > ( x) (a származék definíciója alapján), és így a x> 0 ε / Δ x = 0.Ebből következik, hogy Δ x → 0 ε = 0. Most Δ x → 0 Δ f mint d f és x> 0 Δ x mint d x a különbség meghatározását szigorúan megkapjuk. Például a funkció különbsége. Két vagy több változó funkciói esetén egy függvény teljes differenciálását a független változók irányában lévő differenciálások összegeként határozzuk meg. Matematikailag, .


• A származékot

|
adja. Ajánlott |




