Különbség lineáris és nemlineáris differenciálegyenletek között

lineáris vs Nemlineáris differenciálegyenletek

Egy legalább egy differenciális együtthatót vagy egy ismeretlen változó származékát tartalmazó egyenlet differenciál egyenletként ismert. Egy differenciálegyenlet lehet lineáris vagy nem lineáris. A cikk célja, hogy megmagyarázza, mi a lineáris differenciálegyenlet, mi a nemlineáris differenciálegyenlet, és mi a különbség a lineáris és a nemlineáris differenciálegyenletek között.

A matematikusok, mint a Newton és Leibnitz, a 18. századi kalkulus fejlődését tekintve a differenciálegyenlet fontos szerepet játszott a matematika történetében. A differenciálegyenletek a matematikában nagy jelentőségűek az alkalmazási körük miatt. A differenciálegyenletek mindegyik modell középpontjában állnak, hogy megmagyarázzunk minden forgatókönyvet vagy eseményt a világban, függetlenül attól, hogy fizika, mérnök, kémia, statisztika, pénzügyi elemzés vagy biológia (a lista végtelen). Valójában, amíg a kalkulus nem lett kialakult elmélet, megfelelő matematikai eszközök nem voltak elérhetők a természetben érdekes problémák elemzésére.

A kalkulus egy adott alkalmazásából származó egyenletek meglehetősen bonyolultak és néha megoldatlanok. Azonban vannak olyanok, amelyeket megoldhatunk, de hasonlónak és zavarosnak tűnhet. Ezért a könnyebb azonosító differenciálegyenleteket a matematikai viselkedésük szerint csoportosítják. A lineáris és a nemlineáris egy ilyen kategorizálás. Fontos meghatározni a lineáris és nemlineáris differenciálegyenletek közötti különbséget.

Mi a lineáris differenciálegyenlet?

Tegyük fel, hogy

f: X → Y és f (x) = y, differenciálegyenlet az ismeretlen függvény nemlineáris kifejezései nélkül y lineáris differenciálegyenletként ismert. Olyan feltételt ír elő, hogy y nem lehet magasabb indexszavak, például y

2 ^{, y} 3 ^{, … és a származékok többszörösei, például} Nem tartalmazhat nem lineáris olyan kifejezések, mint a Sin

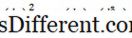
y, e y ^{^ - 2, vagy ln} y. Ez a forma,

ahol

y és g x függvények. Az egyenlet a n rend egyenlet, amely a legmagasabb rendszerszármazék indexe. Egy lineáris differenciálegyenletben a differenciális operátor egy lineáris operátor, és a megoldások vektortartalmat hoznak létre. A megoldás lineáris jellegének eredményeképpen a megoldások lineáris kombinációja is megoldást jelent a differenciálegyenletre.Vagyis ha

y 1 _és y 2 _{a differenciálegyenlet megoldásai, akkor} C 1 _{y < 1} + C ₂ y ₂ megoldás is. _{-2 ->} Az egyenlet linearitása csak a besorolás egyik paramétere, és tovább osztályozható homogén vagy nem homogén és rendes vagy részleges differenciálegyenletekké. Ha a függvény

g

= 0, akkor az egyenlet egy lineáris homogén differenciálegyenlet. Ha f két vagy több független változó (f: X, T → Y) és f (x, t) = y Az egyenlet lineáris parciális differenciálegyenlet.

A differenciálegyenlet megoldási módja a differenciálegyenlet típusától és koefficienseitől függ. A legegyszerűbb eset akkor merül fel, ha az együtthatók állandóak. Klasszikus példája ebben az esetben a Newton második mozgásszabálya és annak különböző alkalmazása. Newton második törvénye egy másodrendű lineáris differenciálegyenletet állít elő állandó koefficiensekkel.

Mi a nemlineáris differenciálegyenlet?

A nemlineáris kifejezéseket tartalmazó egyenleteket nemlineáris differenciálegyenletnek nevezzük.

A fentiek a nemlineáris differenciálegyenletek. A nemlineáris differenciálegyenleteket nehéz megoldani, ezért szoros vizsgálat szükséges a helyes megoldás eléréséhez. Parciális differenciálegyenletek esetén a legtöbb egyenletnek nincs általános megoldása. Ezért minden egyenletet önállóan kell kezelni.

Navier-Stokes egyenlet és Euler egyenlete a folyadékdinamikában, az Einstein általános relativitási téregyenletei jól ismert nemlineáris parciális differenciálegyenletek. Néha a Lagrange egyenlet változó rendszerre történő alkalmazása nemlineáris parciális differenciálegyenleteket eredményezhet.

Mi a különbség a lineáris és a nemlineáris differenciálegyenletek között?

• Egy differenciálegyenlet, amely csak az ismeretlen vagy függő változó lineáris kifejezéseit és származékait ismerteti, lineáris differenciálegyenletnek nevezzük. Az 1-nél nagyobb indexfüggő változónak nincs kifejezésük, és nem tartalmaz semmi származékát. Nem lehet nemlineáris függvények, például trigonometrikus függvények, exponenciális függvények és logaritmikus függvények a függő változóhoz képest. Minden fenti egyenletet tartalmazó differenciálegyenlet egy nemlineáris differenciálegyenlet.

• A lineáris differenciálegyenletek megoldásai vektortartományt hoznak létre, és a differenciális operátor egy lineáris operátor is a vektor térben.

• A lineáris differenciálegyenletek megoldásai viszonylag könnyebbek és általános megoldások léteznek. A nemlineáris egyenletek esetében a legtöbb esetben az általános megoldás nem létezik, és a megoldás problémás lehet. Ez sokkal nehezebbé teszi a megoldást, mint a lineáris egyenleteket.