Különbség párhuzamos és rhombus között: párhuzamosság vs rhombus

Parallelogram vs. Rhombus

A rombusz négyszögletes. Ezeknek a számoknak a geometriája évezredek óta ismeretes az ember számára. A témát kifejezetten az Euclid görög matematikus által írt "Elements" könyvben kezelik.

Parallelogram

A párhuzamos ábrázolás négy oldalas geometriai alakként definiálható, egymással ellentétes oldalakkal párhuzamosan. Pontosabban négyszög, két pár párhuzamos oldal. Ez a párhuzamos természet sok geometriai tulajdonságot biztosít a parallelogrammok számára.

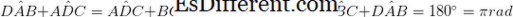
A négyszög egy paralelogramma, ha a következő geometriai jellemzőket találjuk.

• Két pár egymással ellentétes oldala egyenlő hosszúságú. (AB = DC, AD = BC)

• Két pár ellentétes szög egyenlő méretű. (

)

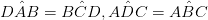
• Ha a szomszédos szögek kiegészítőek

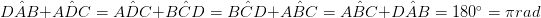
• Egy egymásnak ellentmondó oldal párja párhuzamos és egyenlő hosszúságú. (AB = DC & ABáshozDC)

• Az átló átlósan egymásra (AO = OC, BO = OD)

• Minden átló osztja a négyszöget két egymásnak megfelelő háromszögre. (ΔADB ≡ ΔBCD, ΔABC ≡ ΔADC)

Továbbá az oldalak négyzetének összege megegyezik az átlós négyzetek összegével. Ez néha a parallelogram törvény néven hivatkozik, és széles körben alkalmazható a fizikában és a mérnöki munkában. ⁺ 2 ^{+ DA} 2 ^{= AC} 2 ^{+ BD} 2 ^{+ BC < 2} ) ^{A fenti jellemzők mindegyike tulajdonságként használható, miután megállapították, hogy a négyszög paralelogramma.} A paralelogramma területe az egyik oldal hossza és az ellenkező oldal magassága alapján számítható ki. Ezért a paralelogramma területe

paralelogramma területe = alap × magasság = AB × h

Paramogramogram területe független az egyedi paralelogramm alakjától. Csak az alap és a merőleges magasság függvénye.

Ha a paralelogramma oldalai két vektorral ábrázolhatók, akkor a terület a két szomszédos vektor vektorterméke (keresztterméke) nagyságával nyerhető.

Ha az AB és az AD oldalakat a vektorok () és () reprezentálják, a párhuzamogram területét

adja meg, ahol α a

és.

A következőkben néhány párhuzamossági tulajdonság található:

• A paralelogramma területe kétszerese annak a háromszögnek, amelyet bármelyik átlója létrehoz.

• A paralelogramma területe a fél középponton áthaladó bármely vonal felével van felosztva.

• Minden nem degenerált affin transzformáció párhuzamot mutat egy másik párhuzamogrammal

• A parallelogramnak a 2. sorrendi szimmetriája

• A paralelogramma belső oldalán lévő távolságok összege független a a pont helyzete

Rhombus

A négyszög minden oldalán azonos hosszúságú rhombusnak ismert. Úgy is nevezik, mint

egyenlő oldalú négyszög

. Úgy gondolják, hogy a gyémánt alakja hasonló a játékkártyához.

A Rhombus a paralelogramm különleges esete. Úgy tekinthető, mint egy paralelogramma mind a négy oldal egyenlő. És a következő különleges tulajdonságokkal rendelkezik, a paralelogramm tulajdonságai mellett. • A rombusz átlói egymásra merőlegesen helyezkednek el; az átlós merőleges. • Az átló a két ellentétes belső szöget választja el.

• A szomszédos oldalak közül legalább kettő egyenlő hosszúságú.

A rombusz területét ugyanúgy lehet kiszámítani, mint a parallelogramm.

Mi a különbség a paralelogram és a Rhombus között?

• A paralelogramma és a rombusz négyszögletes. A Rhombus a parallelogrammok különleges esete.

• Minden terület kiszámítható a formula alap × magasság alapján.

• Figyelembe véve az átlósokat;

- A paralelogramma átlói egymásra hatolnak, és két párhuzamos háromszöget alkotnak.

- A rombusz átlói egymásra merőlegesen határolnak, és a háromszögek egyenlő oldalúak.

• Figyelembe véve a belső szöget;

- A párhuzamogramnak a belső szögei ellenére azonos méretűek. Két szomszédos belső szög kiegészítő.

- A rombusz belső szögeit átlósan kettéosztják.

• Figyelembe véve az oldalakat;

- Parallelogrammban az oldalsó négyzetek összege megegyezik az átló négyzetének összegével (Parallelogram law).

- Mivel mind a négy oldal egyenlő a rombuszban, négy oldalas négyzet egyenlő az átló négyzetének összegével.