Különbség Power Series és Taylor sorozat

Power Series vs Taylor Series

A matematikában egy valós sorrend a valós számok rendezett listája. Formálisan a természetes számok halmazából a valós számok halmazához tartozik. Ha a _n egy szekvencia n ^th kifejezés, akkor a a ₁ , ₂ , …, a _n, . Például, fontolja meg az 1, ½, ⅓, …, ¹ / _n sorozatokat. Ez lehet {1 / n}.

Lehetőség van szekvenciák sorozatainak meghatározására. A sorozat a sorrend feltételeinek összege. Ezért minden egyes sorozathoz tartozik egy kapcsolódó szekvencia és fordítva. Ha a {a _n} a vizsgált szekvencia, akkor az adott szekvencia által létrehozott sorozat a következőképpen ábrázolható:

A fenti példában a kapcsolódó sorozat 1+

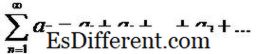
1 ^/ 2 ₊ 1 ^/ 3 _{+ … +} 1 ^/ n _{+ ….} Amint a nevek azt sugallják, a teljesítménysorozat egy speciális sorozatfajta, és széles körben használják a numerikus elemzés és a kapcsolódó matematikai modellezés. A Taylor sorozat egy speciális teljesítménysorozat, amely alternatív és könnyen manipulálható módon ismert funkciókat képvisel.

Mi a Power sorozat?

A teljesítménysorozat a

, ami konvergens (esetleg) bizonyos időközönként

c középpontban. A a n _{együtthatók valós vagy komplex számok lehetnek, és} x-től függetlenek; én. e. a dummy változó. Például, mindegyik

n, és _c = 0 a n = 1 értékkel az 1 + x + x teljesítménysorozatot 2 ^{+ … + x} n ^{+ …. Könnyen megfigyelhető, hogy ha x ε (-1, 1), ez a teljesítménysorozat 1 / (1-x) értékre konvergál.}

Egy teljesítménysorozat konvergál, ha x = c. A x egyéb értékek, amelyekhez a teljesítménysorozat konvergál, mindig nyitott intervallum formájában fognak megjelenni c. ez, 0 < R ≤ ∞ értéket kap, így minden x kielégítő | xc | ≤ R, a teljesítménysorozat konvergens és mindegyik x kielégítő> xc |> R esetén a teljesítménysorozat eltér. Ezt a R értéket a teljesítménysorozat konvergenciasugárának nevezzük (R bármilyen valós értéket vagy pozitív véget érhet).

A teljesítménysorozat hozzáadható, kivonható, megszorozható és felosztható az alábbi szabályok szerint. Tekintsük a két teljesítménysorozatot:

.

Ezután

i. e.

hasonló kifejezések hozzáadásával vagy kivonásával együtt. Továbbá lehetőség van a két teljesítménysorozat többszörözésére és megosztására az identitás felhasználásával,

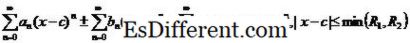
Mi a Taylor sorozat? A Taylor sorozat egy

f

(x) függvényre van definiálva, amely intervallumon belül végtelenül differenciálható. Tegyük fel, hogy f (x) különbözhet a Ezután a A f

(

x) függvény Taylor-sorozatának meghosszabbításáról a c-t jelöli. (n) (c) a ^x = c). A numerikus analízisben a végtelen számú kiterjesztésű kifejezések számát olyan pontok kiszámításakor használják, ahol a sorozat az eredeti függvényhez konvergál. ^A f (x) függvény analitikusnak mondható az intervallumban (a, b), ha minden x ε (a, b), a f (x) Taylor-sorozat konvergál a f (x) függvényhez. Például 1 / (1-x) analitikus (-1, 1), hiszen Taylor tágulása 1 + x + x 2 + … + x n + … konvergál és e x ^{analitikus mindenütt, mivel a Taylor sorozat} e ^x konvergál e ^{x < minden egyes valós számnál} x. Mi a különbség a Power sorozat és a Taylor sorozat között? 1. A Taylor sorozat a teljesítménysorozat speciális osztálya, amely csak olyan funkciókra van definiálva, amelyek bizonyos nyílt intervallumon végtelenül differenciálhatóak. 2. A Taylor sorozat a különleges formát ölti ^{, míg a teljesítménysorozat lehet}