Különbség a párhuzam és a négyszög között: párhuzamosság vs négyszög

Parallelogram vs. Quadrilateral < A négyszögek és a paralelogramok sokszögek, amelyek az euklideszi geometriában találhatók. A párhuzamosság a négyszög speciális esete. A négyszögek lehetnek sík (2D) vagy 3 dimenziós, míg a parallelogrammok mindig sík.

Kvadrilaterális

A négyszög négyoldalas sokszög. Ennek négy csúcsa van, és a belső szögek összege 3600 (2π rad). A négyszögek besorolása önsugaras és egyszerű négyszögletes kategóriákba sorolható. Az önmagát metsző négyszögek két vagy több oldalát keresztezik egymásnak, és kisebb geometriai alakzatok (például háromszögek alakulnak ki a négyszögben).

Az egyszerű négyszögek is domború és homorú négyszögek. A konkáv négyszögek szomszédos oldalai képezik a reflex szögeket az ábrán belül. Az egyszerű négyszögek, amelyek belsőleg nem rendelkeznek reflex szögekkel, konvex négyszögek. A konvex négyszögek mindig mozaikszerűek.

A négyszögek geometriájának nagy része a kezdeti szinteken a konvex négyszögekre vonatkozik. Néhány négyszöglet nagyon ismerős számunkra az általános iskolák napjától. Az alábbiakban egy diagram mutatja a különböző konvex négyszögeket.

Parallelogram

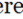
A párhuzamos ábrázolás négyoldalas geometriai alakként definiálható, egymással ellentétes oldalakkal párhuzamosan. Pontosabban négyszög, két pár párhuzamos oldal. Ez a párhuzamos természet sok geometriai tulajdonságot biztosít a parallelogrammok számára.

A négyszög egy paralelogramma, ha a következő geometriai jellemzőket találjuk.

• Két pár egymással ellentétes oldala egyenlő hosszúságú. (AB = DC, AD = BC)

• Két pár ellentétes szög egyenlő méretű. ()

• Ha a szomszédos szögek kiegészítőek

• A pár egymással ellentétes oldala párhuzamos és egyenlő hosszúságú. (AB = DC & ABáshozDC)

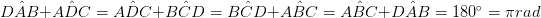
• Az átló átlósan egymásra (AO = OC, BO = OD)

• Minden átló osztja a négyszöget két kongruens háromszögre. (ΔADB ≡ ΔBCD, ΔABC ≡ ΔADC)

Továbbá az oldalak négyzetének összege megegyezik az átlós négyzetek összegével. Ez néha a

parallelogram törvény néven hivatkozik, és széles körben alkalmazható a fizikában és a mérnöki munkában. + ² + DA ² = AC ² + BD ² + BC < 2 ⁾ A fenti jellemzők mindegyike tulajdonságként használható, miután megállapították, hogy a négyszög paralelogramma. ^{A paralelogramma területe az egyik oldal hossza és az ellenkező oldal magassága alapján számítható ki. Ezért a paralelogramma területe} parallelogram területe = alap × magasság =

AB

×

h A párhuzamogram területe független az egyedi paralelogramm alakjától. Csak az alap és a merőleges magasság függvénye. Ha a paralelogramma oldalai két vektorral ábrázolhatók, akkor a terület a két szomszédos vektor vektorterméke (keresztterméke) nagyságával nyerhető. Ha az AB és az AD oldalakat a vektorok (

) és () reprezentálják, a párhuzamogram területét

adja meg, ahol α a

és.

A következőkben néhány párhuzamossági tulajdonság található:

• A paralelogramma területe kétszerese annak a háromszögnek, amelyet bármelyik átlója létrehoz.

• A paralelogramma területe a fél középponton áthaladó bármely vonal felénél van felosztva.

• Minden nem degenerált affin transzformáció párhuzamot mutat egy másik párhuzamogrammal

• A parallelogramnak a 2. sorrendi szimmetriája

• A paralelogramma belső oldalán lévő távolságok összege független a a pont helyzete

Mi a különbség a párhuzamos és a négyszög között?

• A négyszögek négy oldalú poligonok (néha tetragonok), míg a párhuzamos egy speciális négyszögfajta.

• A négyszögletes oldalak különböző síkokban (3d térben) lehetnek, míg a parallelogram összes oldala ugyanazon a síkon (sík / 2dimenziós) fekszik.

• A négyszög belső szögei bármilyen értéket (beleértve a reflex szöget is) érhetnek el, így akár 3600 értéket is adhatnak hozzá. A párhuzamos ábrák csak a szög maximális alakját tekintve lehetnek tompaszögűek.

• A négyszög négy oldala eltérő hosszúságú lehet, míg a párhuzamos nézet ellentétes oldala egymással párhuzamos és egyenlő hosszúságú.

• Bármelyik átló osztja a paralelogrammát két egybevágó háromszögbe, míg az általános négyszög átlója által képzett háromszögek nem feltétlenül egyeznek egymással.