Különbség a párhuzamos és a trapéz között: párhuzamos vagy trapéz (trapéz)

Parallelogram vs trapezoid

A paralelogramma és a trapéz (vagy trapéz) két konvex négyszög. Bár ezek négyszögek, a trapéz geometriája jelentősen eltér a parallelogrammoktól.

Parallelogram

A párhuzamos ábrázolás négy oldalas geometriai alakként definiálható, egymással ellentétes oldalakkal párhuzamosan. Pontosabban négyszög, két pár párhuzamos oldal. Ez a párhuzamos természet sok geometriai tulajdonságot biztosít a parallelogrammok számára.

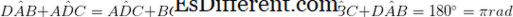
A négyszög egy paralelogramma, ha a következő geometriai jellemzőket találjuk.

• Két pár egymással ellentétes oldala egyenlő hosszúságú. (AB = DC, AD = BC)

• Két pár ellentétes szög egyenlő méretű. (

)

• Ha a szomszédos szögek kiegészítőek

• Egy egymásnak ellentmondó oldal párja párhuzamos és egyenlő hosszúságú. (AB = DC & ABáshozDC)

• Az átló átlósan egymásra (AO = OC, BO = OD)

• Minden átló osztja a négyszöget két egymásnak megfelelő háromszögre. (ΔADB ≡ ΔBCD, ΔABC ≡ ΔADC)

Továbbá az oldalak négyzetének összege megegyezik az átlós négyzetek összegével. Ez néha a parallelogram törvény néven hivatkozik, és széles körben alkalmazható a fizikában és a mérnöki munkában. ⁺ 2 ^{+ DA} 2 ^{= AC} 2 ^{+ BD} 2 ^{+ BC < 2} ) ^{A fenti jellemzők mindegyike tulajdonságként használható, miután megállapították, hogy a négyszög paralelogramma.} A paralelogramma területe az egyik oldal hossza és az ellenkező oldal magassága alapján számítható ki. Ezért a paralelogramma területe

parallelogram területe = alap × magasság =

AB

× h A paralelogramma területe független az egyedi paralelogramm alakjától. Csak az alap és a merőleges magasság függvénye. Ha a paralelogramma oldalai két vektorral ábrázolhatók, akkor a terület a két szomszédos vektor vektorterméke (keresztterméke) nagyságával nyerhető.

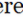
Ha az AB és az AD oldalakat a vektorok () és () reprezentálják, a párhuzamogram területét

adja meg, ahol α a

és.

A következőkben néhány párhuzamossági tulajdonság található:

• A paralelogramma területe kétszerese annak a háromszögnek, amelyet bármelyik átlója létrehoz.

• A paralelogramma területe a fél középponton áthaladó bármely vonal felével van felosztva.

• Minden nem degenerált affin transzformáció párhuzamot mutat egy másik párhuzamogrammal

• A parallelogramnak a 2. sorrendi szimmetriája

• A paralelogramma belső oldalán lévő távolságok összege független a a

Trapezoid

Trapezoid (vagy

Trapezium

angol angol angol pont) helye domború négyszög, ahol legalább két oldal párhuzamos és egyenlőtlen hosszúságú. A trapéz párhuzamos oldalai bázisok néven ismertek és a másik két oldalt lábaknak nevezik.

A trapézek fő jellemzői a következők: • Ha a szomszédos szögek nem a trapéz alapjain találhatók, azok kiegészítő szögek. én. e. 180 ° -ot adnak ()

•

A trapéz két átlója ugyanabban az arányban metszik egymást (az átlós szakaszok aránya egyenlő).

•

Ha a és b alapok és c, d lábak, az átló hosszát és

adja meg. A trapéz területének kiszámítása a következő képlet szerint trapezoid =

Mi a különbség a paralelogram és a trapéz (trapéz) között?

•

Mind a parallelogram, mind a trapéz alakú konvex négyszögek.

•

Egy párhuzamos nézetben mindkét pár párja párhuzamos, míg egy trapéz alakban pár párhuzamos. •

A paralelogramma átlói egymáson hatnak egymásra (1: 1 arány), míg a trapéz átlói metszenek a szakaszok állandó arányával. •

A paralelogramma területe függ a magasságtól és a bázistól, míg a trapéz felületének területe függ a magasságtól és a középső szegmenstől. •

A paralelogrammban lévő diagonok által létrehozott két háromszög mindig egyezik, míg a trapéz háromszögei vagy egybeeshetnek vagy sem.